Master the Math

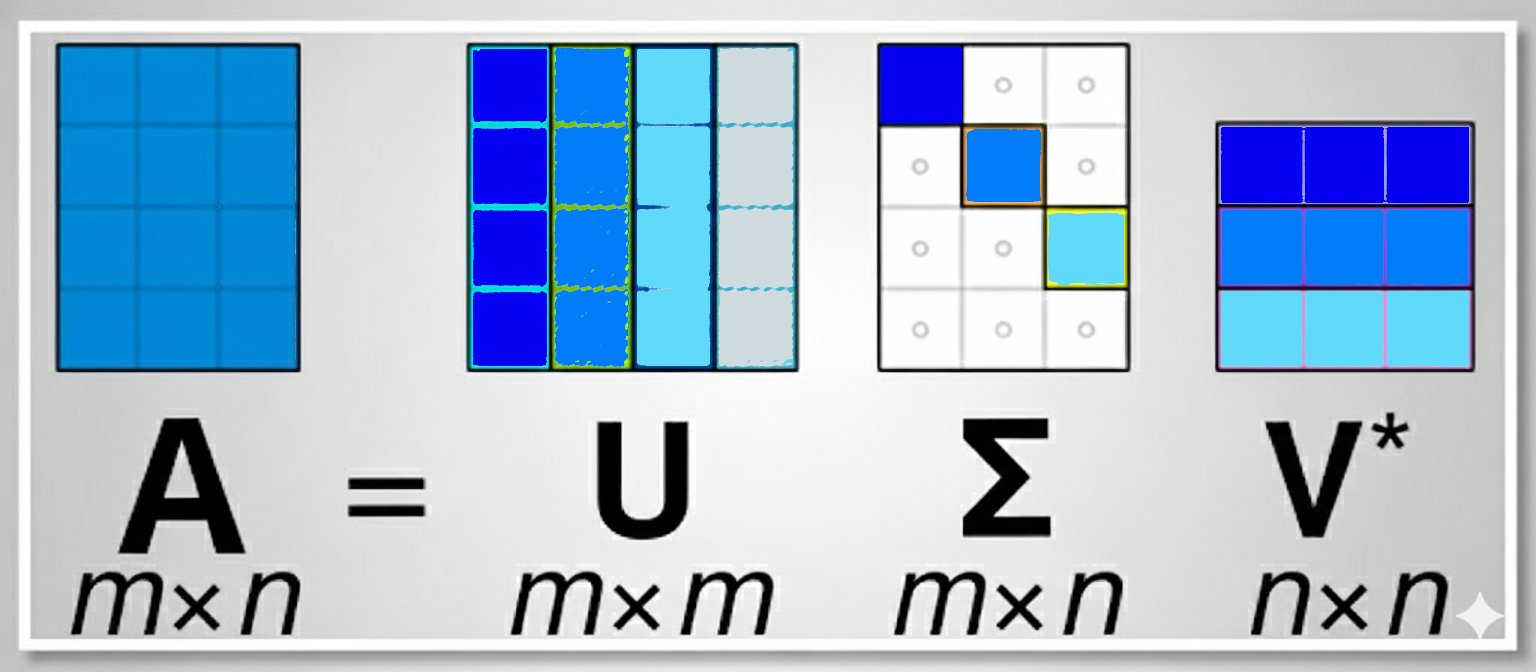
A diagram of the Singular Value Decomposition (SVD) formula showing matrix A being decomposed into matrices U, Sigma, and V-star. The image displays the dimensions of each matrix and uses color-coding to show how specific columns of U, diagonal values of Sigma, and rows of V-star are linked together as sets of triplets.

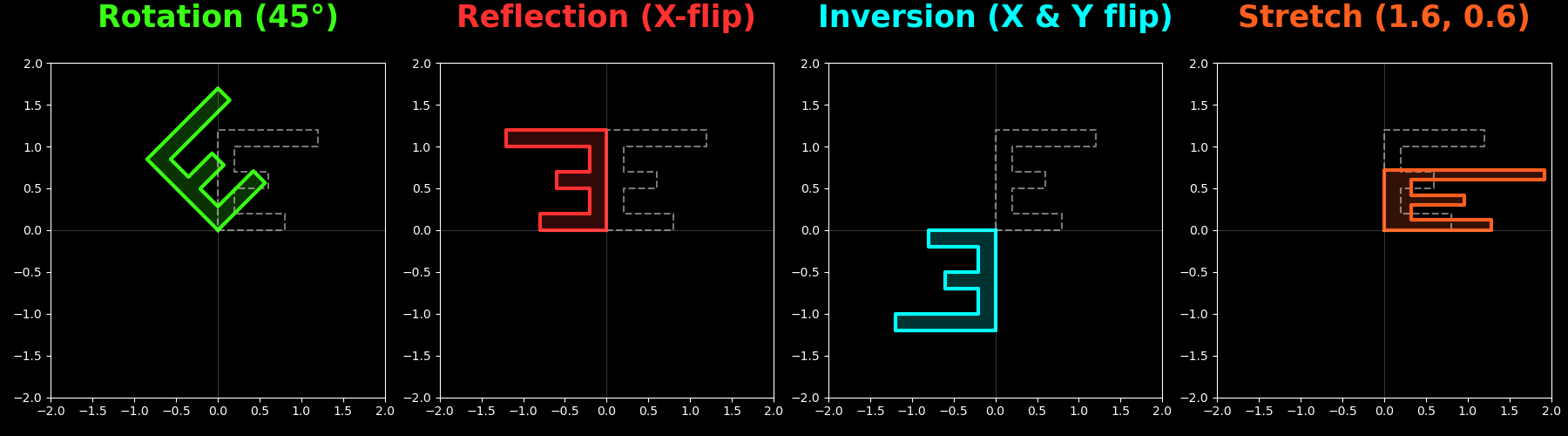
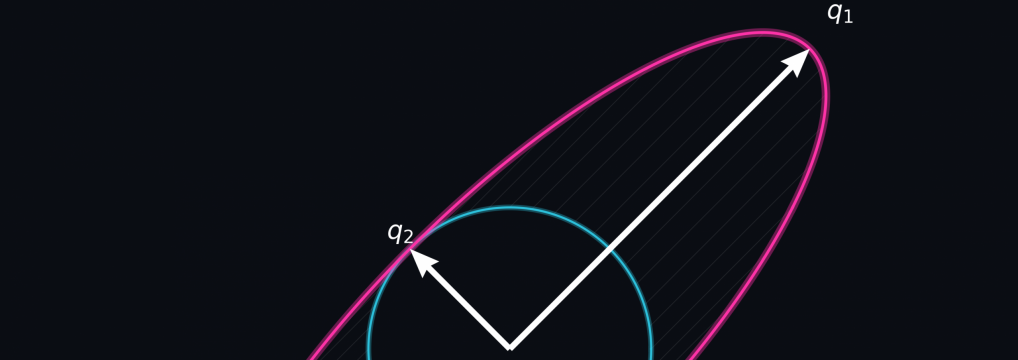
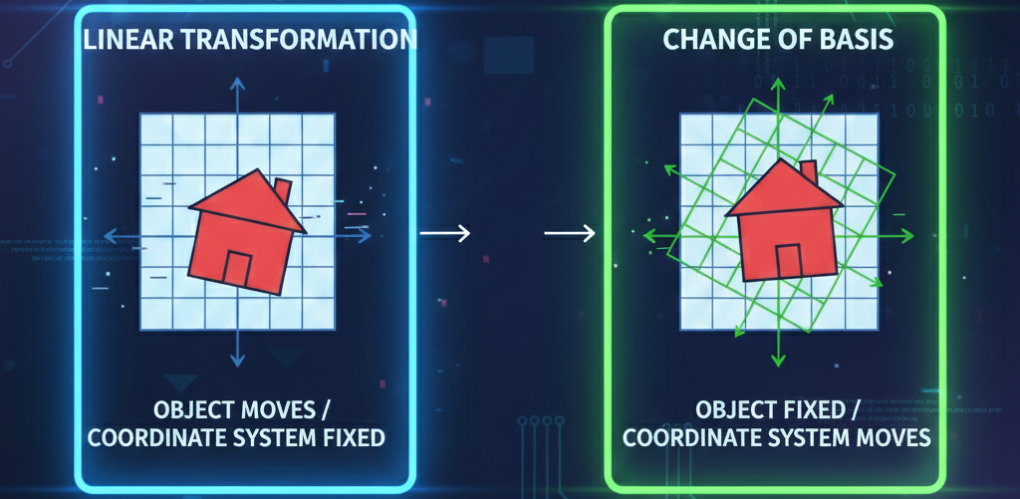
Deriving the Singular Value Decomposition (SVD) from First Principles

The Singular Value Decomposition (SVD) is “a highlight of linear algebra” to quote Prof. Strang ( [1] p. 371). However, I must confess that when I studied it I had a difficult time understanding it and this was due to how it was presented. The SVD is often introduced as a given formula which is then shown to just work. But it always felt very unsatisfying to me not knowing why. So – here is the SVD explained the way I wish I had been taught, which is deriving it from first principles.

Four line graphs on a white background showing 2D geometric transformations of a letter 'E'. From left to right: Rotation (45°), Reflection (X-flip), Inversion (X & Y flip), and Stretch (1.6, 0.6).

Linear Algebra

Understanding the Geometry of Orthogonal and Diagonal Matrices

Why do orthogonal matrices rotate while diagonal matrices stretch?
In this deep dive into linear algebra, we prove the geometric intuition behind the Singular Value Decomposition (SVD). By examining how inner products are preserved and how basis vectors are scaled, I demonstrate why linear transformations are restricted to these specific movements.

$Geometric visualization of spectral decomposition showing the transformation of a unit circle into an ellipse with orthogonal eigenvectors $\mathbf{q}_1$ and $\mathbf{q}_2$.$